I've always been interested in phone keypad sounds, so I tried to replicate them. Here's what I managed to work out just by ear:
- Each key has a unique sound
- The unique sound is made up of two pitches
- The tone generated is a pure sine wave
- The tones aren't using equal temperament.
The most interesting thing to me was that the tones weren't using equal temperament – i.e., they wouldn't line up perfectly with notes on a piano or guitar.
To test my ears, I tried to work out the pitches each key made. Using a MIDI keyboard and some synthesizer software, I configured a polyphonic synthesizer to play a simple unfiltered sine wave for each note pressed.
Here are the notes I approximated for each row on the keypad:
Top row:
1⃣ F5 + D6
2⃣ F5 + E6
3⃣ F5 + F♯6
Second row:
4⃣ G5 + D6
5⃣ G5 + E6
6⃣ G5 + F♯6
Third row:
7⃣ A♭5 + D6
8⃣ A♭5 + E6
9⃣ A♭5 + F♯6
Fourth row:
*⃣B♭5 + D6
0⃣B♭5 + E6
#⃣B♭5 + F♯6
For each row on the keypad, the lower pitch rises moving downwards; and for each column the higher pitch rises moving right.
While working out these approximations, I was very aware of some notes that were particularly far from the equal-tempered western scale. For instance, the higher tone corresponding to the leftmost column seems somewhat sharp compared to a Western D6. Even more strikingly, the lower note I decided was closest to a G5 (for the second row) sounded incredibly flat, and I nearly decided it was closer to an F♯5. However, the lower tone of the top row did sound almost indistinguishable from a real equal-temperament F5.
I resorted to Wikipedia to see if my three observations were reasonable.
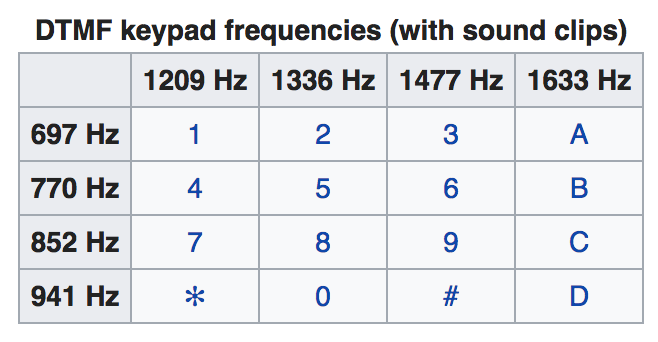
Firstly, the leftmost column's higher tone is 1209Hz. This is 34Hz sharp of the 1175Hz of a Western D6, or about 48 cents* – so I'm not surprised I noticed it!
Secondly, the striking flatness I heard in the second row's lower tone is much subtler than imagined – a difference of only 14Hz! This is somewhat surprising and I'm not sure why that difference jumped out to me so much more than that of the leftmost column's higher tone.
Finally, the top row's lower tone is in reality 697Hz. This is incredibly close to the 699Hz of F5, so at least I'm glad I didn't think that was too far out of tune!
Interestingly, another wide gap between western tuning and the phone keypads I didn't notice at all was that between A♭5 (831Hz) and the third row's 852Hz – a difference of 21Hz total.
Of course, this whole exercise is just part of my evil plan to be able to recognise phone numbers just by hearing them. Give me a call if you can decipher my phone number from these sound clips!
* Napkin maths: I'm not sure if semitone cents are usually calculated logarithmically – that'd make sense! – but in this case the difference is probably too small to worry about. I just split the difference between the two frequencies into 100 equal slices, and calculated that 34Hz out of 70Hz was about 48%. I'd be interested to do the maths though, as that does seem extremely sharp for what seemed to me a pitch that was much closer to the lower note.
* Napkin maths part 2: I did the calculations again using logarithmic cents! The first difference was 49 cents, so again, not surprising to have noticed it. The second "subtler" difference was 31 cents, so I'm still at a loss to realise why that seemed more striking to me, but I'm glad it's not a really tiny difference. On the other hand, the wide gap I didn't notice between 831Hz and 852Hz works out to be just over 43 cents, so still an extremely wide gap to have missed! Maybe I need to practice tuning my instruments more...